최대 부분 증가수열
N개의 자연수로 이루어진 수열이 주어졌을 때, 그 중에서 가장 길게 증가하는(작은 수에서 큰
수로) 원소들의 집합을 찾는 프로그램을 작성하라. 예를 들어, 원소가 2, 7, 5, 8, 6, 4, 7,
12, 3 이면 가장 길게 증가하도록 원소들을 차례대로 뽑아내면 2, 5, 6, 7, 12를 뽑아내어 길
이가 5인 최대 부분 증가수열을 만들 수 있다.
▣ 입력설명
첫째 줄은 입력되는 데이터의 수 N(2≤N≤1,000, 자연수)를 의미하고,
둘째 줄은 N개의 입력데이터들이 주어진다.
▣ 출력설명
첫 번째 줄에 부분증가수열의 최대 길이를 출력한다.
▣ 입력예제 1
8
5 3 7 8 6 2 9 4
▣ 출력예제 1
4
문제풀이
import sys
sys.stdin=open("input.txt", "r")
n = int(input())
arr=list(map(int, input().split()))
arr.insert(0,0)
dy=[0]*(n+1)
dy[1]=1
res=0
for i in range(2, n+1):
max =0
for j in range(i-1, 0, -1): #0직전인 1까지 탐색
if arr[j]<arr[i] and dy[j]>max:
max=dy[j]
dy[i]=max+1
if dy[i]>res:
res=dy[i]
print(res)▶ 모르면 디버깅을 해봐라.★
다만 안쪽 for문을 다 돌은 경우 max=0으로 초기화 됨을 주의하자★
▶ arr[ j ] 는 arr[ i ]앞에 있는 숫자들을 의미한다.
▶ dy[ j ]의 의미 : j번째 숫자(=arr[ j ])를 마지막항으로 두었을 때 가장 긴 증가수열의 길이
▶ dy[ i ]=max+1 의 의미 : 가장 긴 증가수열 길이에 i번째 마지막항(arr[ i ]) 1개를 더한 길이
▶ dy[ i ]의 의미 : i번째 숫자(=arr[ i ])를 마지막항으로 두었을 때 가장 긴 증가수열의 길이
▶ if 조건을 만족하지 않는다면 max+1 즉 max에 마지막항 arr[i] 1개가 붙어서
증가수열의 길이를 증가시킨다.
▶ for j in range(i-1, 0, -1) ← arr[i]보다 앞에 있는 요소를 scan하고 싶을 때★★
문제 해설
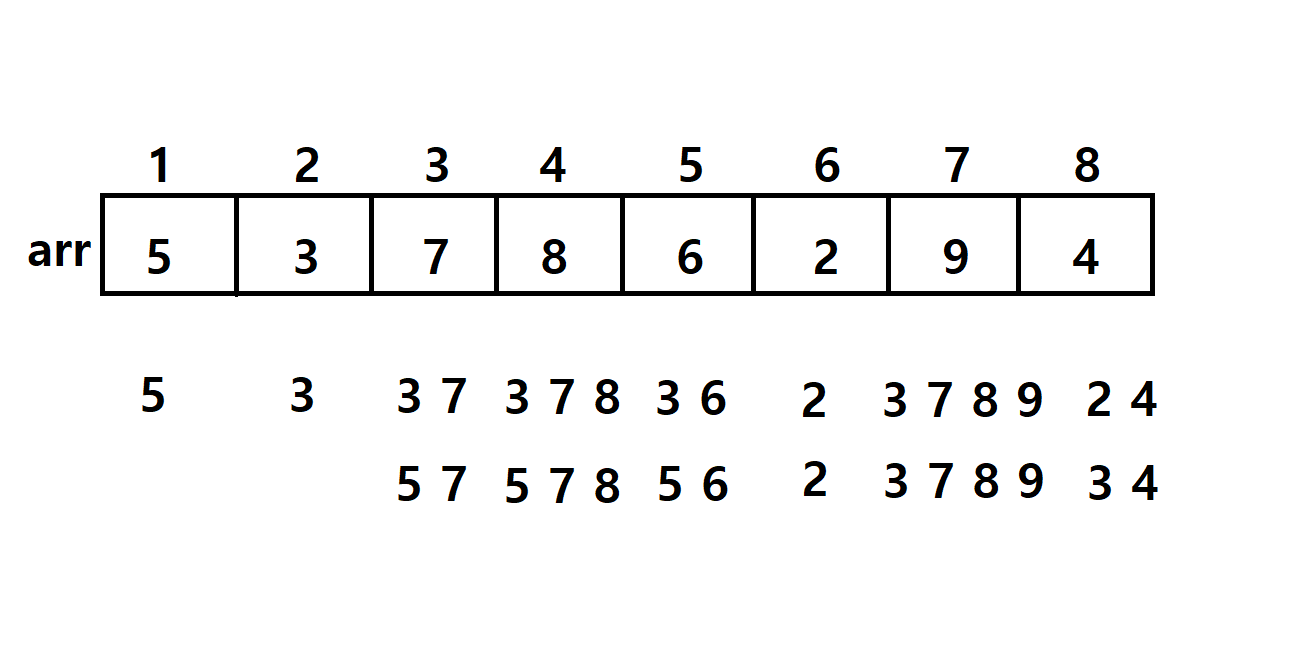
▶ n인덱스에 있는 숫자가 내가 만들고자 하는 증가수열의 마지막항이라고 생각하고 증가수열을 만든다.
▶ 5가 마지막 항인 경우 증가수열은 5하나뿐
▶ 3이 마지막 항인 경우 증가수열은 3 하나뿐
▶ 7이 마지막 항인 경우 3은 증가수열의 앞부분이 될수 있다.
→3이 마지막 항인 경우 만들수 있는 증가수열을 가지수는 1개
3 7
▶ 7이 마지막 항인 경우 5는 증가 수열의 앞부분이 될 수 있다.
→5가 마지막항인 경우 만들 수 있는 증가수열의 가지수는 1개
5 7
▶ 8이 마지막항인 경우 앞에 7이 올수 있다.
→7이 오는 경우 3 7 또는 5 7에 8이 붙을 수 있다.
즉 3 7 8 , 5 7 8 을 만들 수 있다.
▶ 8이 3이나 5뒤에 붙어서 3 8 또는 5 8을 만들 수 있다.
하지만 이러한 경우는 가장 긴 증가수열을 만들수 있는 경우에
해당하지 않기 때문에 고려하지 않는다.
▶ 9이 마지막항인 경우 앞에 있는 8에 붙어야 가장 긴 증가수열을 만들 수 있다.
→3 7 8 9 , 5 7 8 9를 만들 수 있다.

▶ dy[1] 의 의미→5이 내가 만들고자하는 증가수열의 마지막일 때 가장 긴 수열의 길이
▶ dy[2] 의 의미→3이 내가 만들고자하는 증가수열의 마지막일 때 가장 긴 수열의 길이
▶ dy[3] 의 의미→7이 내가 만들고자하는 증가수열의 마지막항일 때 가장 긴 수열의 길이(갯수가 아님)
▶ 9는 가장 긴 수열 8에 붙어야 9가 증가수열의 마지막항일 때 가장 긴 수열의 길이를 갖을 수 있다.
8의 증가수열길이의 길이 3에다가
9가 추가적으로 붙으므로
즉 길이가 +1늘어나므로 9가 증가수열의 마지막항일 때 증가수열의 길이는 4이다.
보충자료

'파이썬 알고리즘 > 동적계획법' 카테고리의 다른 글
| 6. 가장 높은 탑 쌓기(LIS 응용) (0) | 2022.11.23 |
|---|---|
| 5. 최대 선 연결하기(LIS응용) -디버깅해보자 (0) | 2022.11.23 |
| 3. 돌다리 건너기(Bottom-Up) (0) | 2022.11.23 |
| 2.네트워크 선 자르기(Top-Down방식) (0) | 2022.11.23 |
| 1. 네트워크 선 자르기(Bottom-Up) (0) | 2022.11.23 |
